Multi-fidelity Optimisation: The art of skimming
If you had 3 days to find the best book in a pile of 100 books with unknown authors and titles, how would you do it? You would not have the time to read all of them from cover to cover. Even a speed-reading professional may find the task tedious.
You could decide to skim (read quickly) all of them, starting with the introduction and conclusion, then reading a few selected chapters. Yet, with this approach, you would not read any of the books in full, which may affect the quality of your judgement.
This type of reasoning can be applied to optimisation problems, in which we try to find a solution that maximises or minimises a function, called the objective or evaluation function. For more on optimisation, you can check out the other articles in this series.
In most difficult problems, it is impossible to evaluate all possible combinations. In some even harder problems, evaluating a single solution is costly. But what if, like books, you could “skim” a solution and get an idea of how good it is?
As an example, if you are trying to optimise the structure of a deep learning model, a single retraining may cost hours of computing time. However, you can always get early indications of model performance such as validation metrics at certain epochs.
In a different field, the full drug testing process is very expensive. Yet, it is possible to get cheaper indicators of a molecule’s effect, such as simulations and quantitative analysis. You could apply these simulations to a large number of compounds, and only test the compounds most likely to be effective.
The same applies to books.
Successive Halving to the rescue
Going back to our books, what would be a good approach to blend the speed of skimming with the precision of a full read?
One strategy would be to:
- Skim all 100 books, dedicating 20 minutes to each book → already 33 hours.
- From this skimming, discard the “worst” 50 books, and dedicate another 20 minutes to each of the remaining books → adding another 17 hours to the search process, only 32 hours remaining.
- After this session and a few cups of coffee, keep only the best 25 books and spend another 20 minutes reading them → another 8 hours.
- Repeat the process until you either fall asleep or reach the end of the allotted time.
The following chart shows the book quality as a function of time spent reading; each line represents a single book. Lines are cut short when the book is discarded.
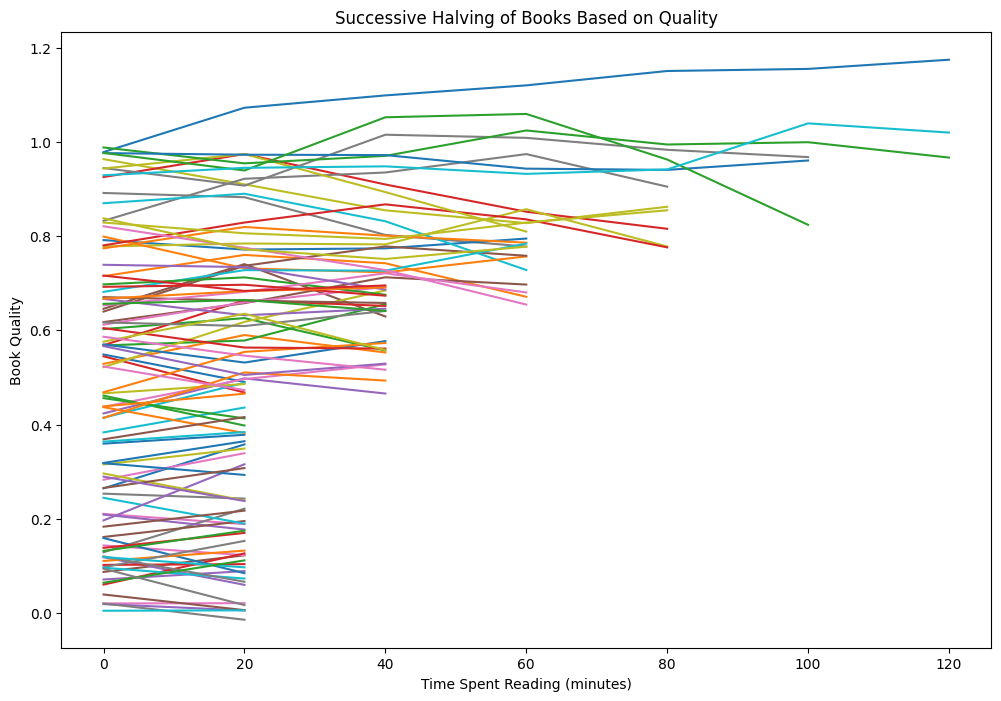
Code used to generate the plot
import numpy as np
import matplotlib.pyplot as plt
# Parameters
num_books = 100
time_per_increment = 20
total_time = 120 # Total time to fully read a book
num_iterations = total_time // time_per_increment
# Initialize book qualities
np.random.seed(0) # For reproducibility
books = {}
for i in range(num_books):
books[i] = {
'times': [0],
'qualities': [np.random.uniform(0, 1)],
'active': True
}
# Successive Halving Process
for iteration in range(1, num_iterations + 1):
# Get list of active books
active_books = [i for i, b in books.items() if b['active']]
if not active_books:
break
# Simulate quality improvement with minor fluctuations
for i in active_books:
prev_quality = books[i]['qualities'][-1]
new_quality = prev_quality + np.random.normal(0, 0.05)
books[i]['qualities'].append(new_quality)
books[i]['times'].append(iteration * time_per_increment)
# Discard the bottom half
num_to_keep = len(active_books) // 2
sorted_books = sorted(active_books, key=lambda x: books[x]['qualities'][-1], reverse=True)
books_to_discard = sorted_books[num_to_keep:]
for i in books_to_discard:
books[i]['active'] = False
# Plotting
plt.figure(figsize=(12, 8))
for i, b in books.items():
if len(b['times']) > 1:
plt.plot(b['times'], b['qualities'], label=f'Book {i}')
plt.xlabel('Time Spent Reading (minutes)')
plt.ylabel('Book Quality')
plt.title('Successive Halving of Books Based on Quality')
plt.show()This approach could also be applied to choose the best TV show. You could start from a list of 20 shows, watch the first two episodes of each, then continue watching the next two of the best 10, and repeat the process until only one remains.
You may notice that there are several parameters to choose:
- The initial number of combinations → the number of books considered at the start, here 100.
- The evaluation budget increment → the reading time added at each iteration, here 20 minutes.
This process is called Successive Halving (SH). For once, computer scientists were able to name something properly. Some more advanced methods like Hyperband were later developed to automate the selection of these parameters, but this is outside the scope of this article. All of these methods belong to the family of multi-fidelity methods.
The main idea of Successive Halving is to:
- Start with a large set of combinations, get a quick indicator of their quality
- Discard the bottom half
- Repeat the process with progressively more expensive evaluations until reaching full evaluation
Applying multi-fidelity to other search methods
Multi-fidelity evaluation methods can easily be adapted to other optimisation methods. For instance, how would you add multi-fidelity evaluation to grid and random search?
For grid search, you could consider the entire grid of combinations at once and apply Successive Halving. This would save significant computational cost. In the case of the 100 books read in 20-minute increments, we save 8,080 minutes compared to full evaluation (see calculations below).
- Without SH (full evaluation):
- Total time = Number of books × Time per book: \(100 \times 120 = 12,000\) minutes
- With SH:
- Iteration 1: \(100\) books × \(20\) minutes = \(2,000\) minutes
- Iteration 2: \(50\) books × \(20\) minutes = \(1,000\) minutes
- Iteration 3: \(25\) books × \(20\) minutes = \(500\) minutes
- Iteration 4: \(12\) books × \(20\) minutes = \(240\) minutes
- Iteration 5: \(6\) books × \(20\) minutes = \(120\) minutes
- Iteration 6: \(3\) books × \(20\) minutes = \(60\) minutes
- Total time with SH = \(2,000 + 1,000 + 500 + 240 + 120 + 60 = 3,920\) minutes
- Time saved: \(12,000 - 3,920 = 8,080\) minutes
A similar approach can be used for random search, in which randomly selecting combinations and applying Successive Halving evaluation would enable the search algorithm to consider many more books than a naïve random search.
Just like grid search, it would take 12,000 minutes to read 100 books. As shown above, using Successive Halving, you could evaluate 100 books in 3920 minutes only. Repeating the process three times, you could explore 300 books in less time than what it would take to fully evaluate 100 books.
Now, how would you implement multi-fidelity optimisation with hill climbing or genetic algorithms? Both of these methods involve evaluating groups of solutions. With the hill climbing process, you sample and evaluate the neighbourhood of the current solution.
In genetic algorithms, you may need to evaluate the starting population or a batch of children. Any process involving the evaluation of more than one combination/solution can be done with Successive Halving.
Assumptions of multi-fidelity
Does this process come for free? Can we improve over uninformed search without making any assumptions?
Unfortunately, to use multi-fidelity evaluation, we have to assume that the low-fidelity evaluation of a solution is highly correlated with its full evaluation.
Mathematically, we assume that the correlation between the low-fidelity evaluation \(L(s)\) and the high-fidelity evaluation \(H(s)\) of a solution \(s\) is high:
\[ \operatorname{corr}(L(s), H(s)) \approx 1 \]
If this assumption is met, then multi-fidelity enables significant computation saving.
Final Thoughts
Once again, the more information about a problem we can leverage, the easier it becomes. Think about it when choosing your next book.