The Intuition Behind Optimisation
What should I do with my life? What broadband internet subscription should I choose? Most of our daily problems can be framed as optimisation problems.
Many problems we deal with regularly are optimisation problems. The recurrent question: “How best to spend our time?” can also be phrased as an optimisation problem: maximising our life satisfaction (whatever this means) with respect to the (unknown) amount of time we still have to live.
The task of optimisation refers to minimising or maximising a given function, with respect to a set of constraints. In other words, the idea is to minimise or maximise a quantity such as satisfaction, costs, profits; taking into account a set of constraints, i.e., requirements that must be met.
As an example, when reading a restaurant menu, a customer tries to maximise satisfaction within their dietary requirements and budget constraints. A firm will work to minimise its costs while maximising its revenue, subject to its production constraints such as the number of workers employed or the production capital.
This post develops an intuition for optimisation problems and approaches; the following articles will formalise the problem mathematically and explore various optimisation mehtods such as: gradient descent, linear programming and heuristic search.
How to Solve an Optimisation Problem?
There are many ways to approach an optimisation problem. Let’s explore this with choosing an internet broadband provider.
Choosing Between a Limited Set of Options
Suppose you have three different plans from three different providers:
| Provider | Price | Download Speed | Upload Speed |
|---|---|---|---|
| Provider A | $50 per month | 100 Mbps | 20 Mbps |
| Provider B | $60 per month | 200 Mbps | 50 Mbps |
| Provider C | $55 per month | 150 Mbps | 30 Mbps |
There are several ways to choose. The first is to see if one of the options dominates the others in every regard, such as price, quality of service, etc. If one exists, this is a quick problem to solve.
If no clear winner emerges, the consumer will face some trade-offs. To address them, they can informally assign a utility value (i.e., satisfaction derived from) to each item of the plan like download and upload speed in Mbps. They can also formulate constraints to restrict the options; e.g., “My download and upload speed cannot be lower than 50 Mbps.”
As an example, a customer could value:
- Plan A with download speed 100 Mbps at $20 (as this is too low for their work)
- Plan C with download speed 150 Mbps at $50 per month
- Any plan with a higher download speed (e.g., Plan B) will have the same value of $50 to them as they would not make use of it
To choose a plan, they would compute the satisfaction brought by each plan (see above) minus their cost (defined earlier) and rank the options.
- Plan A: \(\$20 - \$50 = -\$30\), not great
- Plan B: \(\$50 - \$60 = -\$10\), better
- Plan C: \(\$50 - \$55 = -\$5\), still not ideal but the best on the list
Based on these calculations, the customer would choose Plan C and remain slightly disappointed.
This example is still simple as it only has a small number of plans, restricting the number of possible plans to consider.
Internet Plans in a Continuous Space
A continuous version of this problem, in which a customer could select the exact download and upload speed, is trickier to solve. It would then become impractical to consider every possible combination of download and upload speeds.
An interesting way to do so would be to consider the satisfaction brought by each additional Megabit per second of download speed. For simplicity, this example will focus on download speed only.
Let’s imagine that a customer values each additional Mbps of download speed at $0.5 until 200 Mbps, and $0 beyond that.
Utility Function
Plotting the above mentioned utility function, we get:
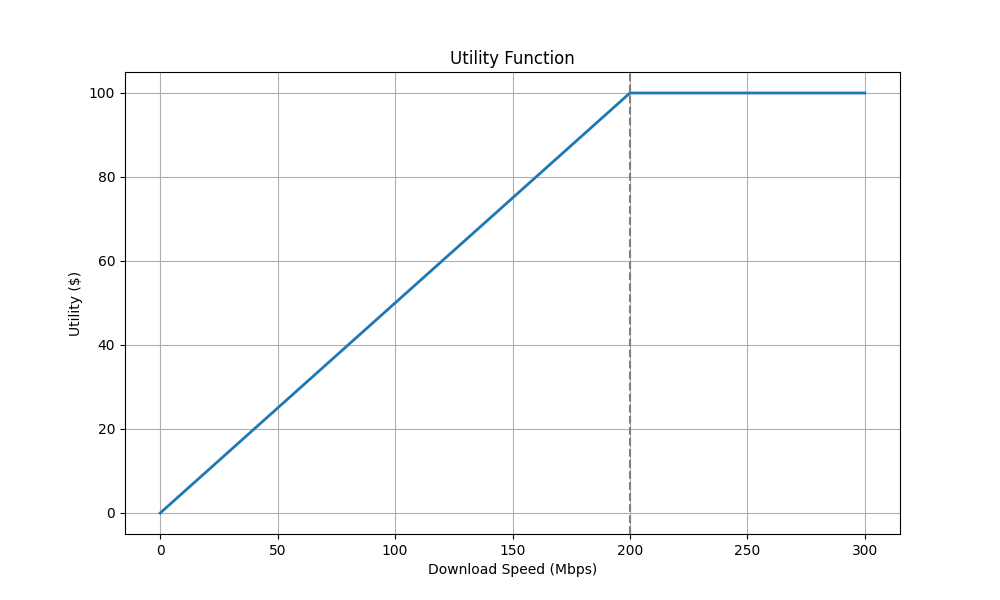
Definition of the utility function
\[ Utility(x) = \begin{cases} 0.5x, & \text{if } x \leq 200 \\ 100, & \text{if } x > 200 \end{cases} \]
Python code used to generate the chart
import numpy as np
import matplotlib.pyplot as plt
# Utility function
def utility(x):
return np.where(x <= 200, 0.5 * x, 100)
# Generate x values
x = np.linspace(0, 300, 301)
# Compute utility values
u = utility(x)
# Plot
plt.figure(figsize=(10, 6))
plt.plot(x, u, linewidth=2)
plt.title('Utility Function')
plt.xlabel('Download Speed (Mbps)')
plt.ylabel('Utility ($)')
plt.axvline(x=200, color='gray', linestyle='--')
plt.grid(True)
plt.show()Cost Function
For our simple example, the plan cost as a function of download speed can be defined by the following function:
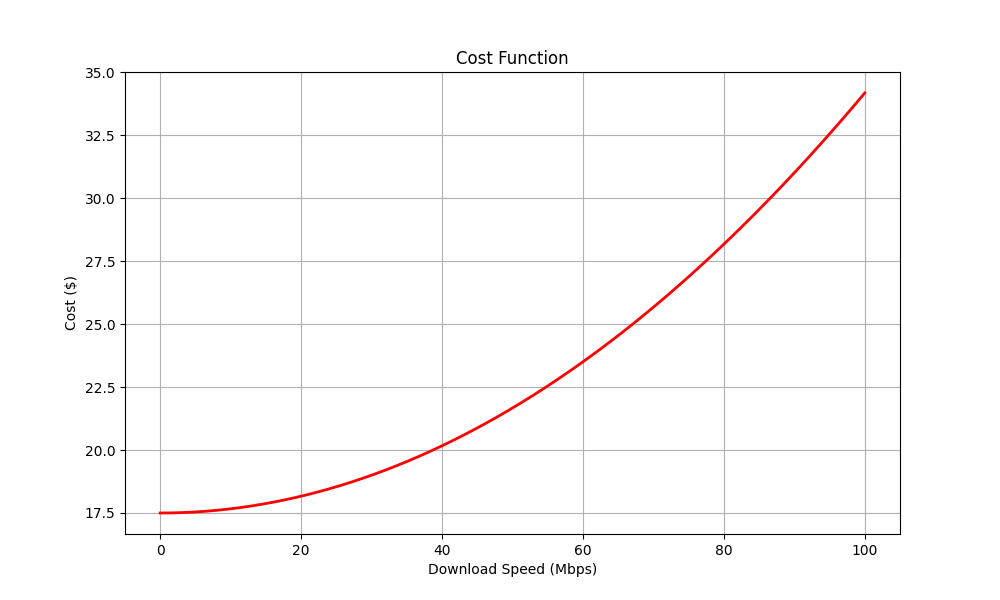
Definition of the cost function
\[ Cost(x) = 1.5x + 0.01(x - 90)^2 + 30 \]
Python code used to generate the chart
# Cost function
def cost(x):
return (1/600) * x**2 + 17.5
# Compute cost values
c = cost(x)
# Plot
plt.figure(figsize=(10, 6))
plt.plot(x, c, color='red', linewidth=2)
plt.title('Cost Function')
plt.xlabel('Download Speed (Mbps)')
plt.ylabel('Cost ($)')
plt.grid(True)
plt.show()Net Utility Function
In this scenario, consumers would be maximising their utility/satisfaction minus the costs they pay. The net utility function is plotted below.
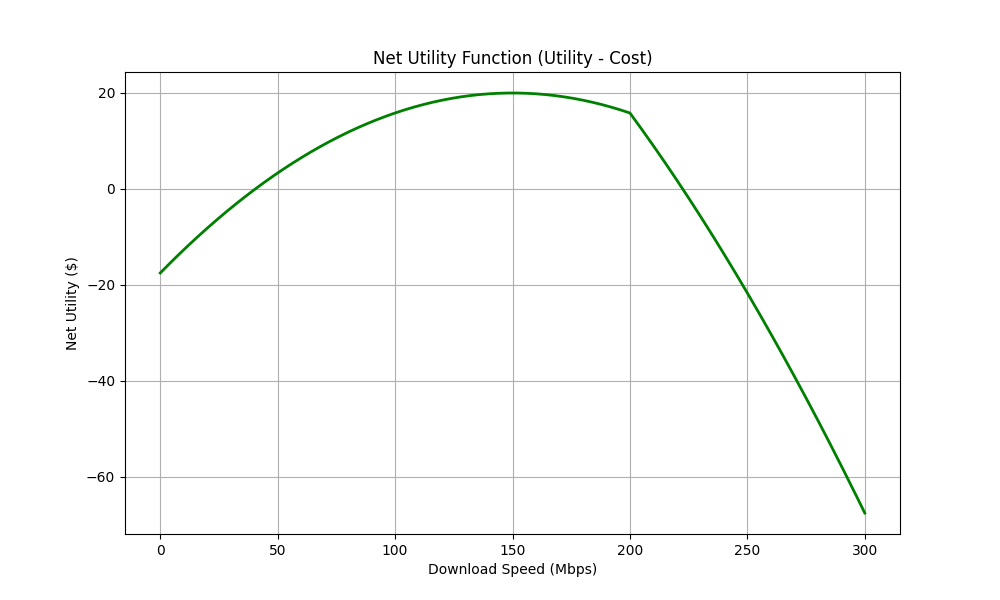
Definition of the net utility function
\[ NetUtility(x) = Utility(x) - Cost(x) \]
Python code used to generate the chart
# Net utility function
def net_utility(x):
return utility(x) - cost(x)
# Compute net utility values
nu = net_utility(x)
# Plot
plt.figure(figsize=(10, 6))
plt.plot(x, nu, color='green', linewidth=2)
plt.title('Net Utility Function (Utility - Cost)')
plt.xlabel('Download Speed (Mbps)')
plt.ylabel('Net Utility ($)')
plt.grid(True)
plt.show()Plotting the function is a way to visually try all combinations. This method still works with a number of decision variables up to 2, as plotting 4 or more dimensions is difficult.
Choosing in the Dark
What if the cost function was unknown and could not be plotted? Let’s say, for instance, that you could go to a provider’s website, enter your desired download and upload speed on its pricing calculator, and it would output a price. How can we search the space of possibility?
Why not test a thousand random combinations? This is not as bad as it sounds. In many optimisation problems, the random search method is a hard benchmark to beat. It is also very simple to implement. You could pick 100 random combinations of download/upload speeds, and check their cost. At the end of all the trials, you pick the combination with the highest utility minus cost value.
You could also try a grid of combinations of download and upload speeds. This would try combinations of upload/download speeds in increments of 10 Mbps. This would significantly reduce the size of the search space.
The table below is a grid of upload/download speeds using 10 Mbps increments in the range 0–100 Mbps:
| Download Speed (Mbps) | Upload Speed (Mbps) |
|---|---|
| 0 | 0 |
| 0 | 10 |
| 0 | 20 |
| ⋮ | ⋮ |
| 10 | 0 |
| 10 | 10 |
| 10 | 20 |
| ⋮ | ⋮ |
| 100 | 90 |
| 100 | 100 |
These methods are the main uninformed search methods. They treat the function to optimise as a “black box”, taking decision variables as inputs and returning an objective function value as output. This is much more computationally intensive than finding the optimal value using analysis or plotting functions, but sometimes, this is the best we can do.
The other articles of this series will explore a range of other methods to search the solution space of black-box optimisation problems, including heuristic search and genetic algorithms.
Making Sense of Optimisation Methods
The optimisation methods we can use depend on the information we have about the problem. The more information we have, the less we have to compute. In the best scenario, we can find the maximum (or minimum) of an objective function using calculus. In the worst-case scenario, we can only observe the objective function value for a given solution. Then, we could resort to random or grid search to explore the search space.
There are many other ways to explore the search space, such as linear programming or heuristic search. If that sounds interesting, head over to part two for a gentle introduction to optimisation methods.