How to analyse the complexity of a Python code snippet?
There is a lot of theory behind algorithm analysis and complexity. But how do these concepts relate to the code you are writing every day?
The goal of this post is to analyse the complexity of actual Python code snippets using the tools shown in the first two parts (intuition, maths) of this series. By the end of it, you should be able to analyse the complexity of any simple code snippet. Let’s get started!
Part 1 of this series developed an intuition for algorithm complexity. To do so, it described the complexity of various tasks associated with organising a party, as the number of guests \(n\) grows to infinity.
These tasks include:
- Greeting each guest as they arrive - link
- Introducing each incoming guest to each guest already present - link
- Playing a game of “Who’s Who?” - link
- Taking pictures of every combination of guests - link
If you need a refresher, the links will bring you to the relevant sections of the first part.
This complexity analysis will rely on the Random Access Machine (RAM, not to be confused with computers’ Random Access Memory) model of computation. This model assumes that the following operations can be done in constant time:
- Reading and writing an element of an array
- Basic arithmetic operations: e.g., addition, subtraction, multiplication, comparison
- Basic system commands: e.g., prints, reading environment variables
The time complexity of an algorithm is then expressed as the total number of these constant time operations as the input size \(n\) grows towards infinity. For the mathematical details of asymptotic notation, please review part 2 of this series.
Greetings
To implement the task of greeting every incoming guest, a simple Python for loop over the guest_list will do.
all_guests = 100
for guest in range(all_guests):
print(f"Hello guest number {guest}, welcome to my party")To understand the complexity of any code snippet, it is important to get an understanding of the number of times each line will run, and the cost incurred by each line; i.e., number of constant time operations required.
Annotating the cost next to each line, we get:
all_guests = 100 # cost: 1
for guest in range(all_guests): # cost: n, the number of guests
print(f"Hello guest number {guest}, welcome to my party") # cost: nWe can write the cost (time complexity) of the algorithm as a function of \(n\), the number of guests. We get: \(f(n) = 1 + 2n\). Using our knowledge of asymptotic notation, we conclude that \(f(n) = O(n)\).
If you do not want to read this short article on asymptotic notation, you can simply identify the fastest growing term (\(2n\)), drop the constant (\(2\)), and we get a final upper-bound time complexity of \(O(n)\).
In most real-life applications, it is impossible to know the number of times a line will run before running the entire program. In that case, it is common practice to identify the worst-case scenario (i.e., highest number of times the line will run) and the best-case scenario. This can then be used to determine the upper-bound complexity. By leveraging probabilities, you can also compute the average-case time complexity, working with the expected runtime of the program.
Introducing Guests
The task of introducing incoming guests to each guest already present is trickier. This task can be implemented with the following code snippet:
all_guests = 100
guests_present = 0
for arriving_guest in range(all_guests):
for guest_present in range(guests_present):
print(f"Hi {guest_present},
have you met {arriving_guest}?")
guests_present += 1Annotating the cost next to each line, we get:
all_guests = 100 # cost: 1
guests_present = 0 # cost: 1
for arriving_guest in range(all_guests): # cost: n
for guest_present in range(guests_present): # cost: 0 + 1 + ... + (n-2) + (n-1)
print(f"Hi {guest_present},
have you met {arriving_guest}?") # cost: same as above
guests_present += 1 # cost: same as aboveBefore putting these costs together, it is important to note that the sum of all integers from \(1\) to \((n-1)\) is:
\[\sum_{i=1}^{n-1} i = \frac{(n-1)n}{2}\].
This can be derived from the sum of all integers from \(1\) to \(n\), \(\frac{n(n+1)}{2}\), replacing \(n\) by \(n-1\).
We then get: \[f(n) = 2 \cdot 1 + n + 3 \cdot \frac{(n-1)n}{2}\]
Expanding: \[f(n) = 2 + n + \frac{3(n^2 - n)}{2} = \frac{3}{2} \cdot n^2 - \frac{1}{2} \cdot n + 2\]
To find the upper-bound time complexity of this formula using asymptotic notation, we can identify the fastest growing term, drop the constant, and get a time complexity of \(O(n^2)\).
Generally, for loops within for loops (also called “nested loops”) are associated with polynomial time complexities.
As a practice problem, prove that the following snippet is of complexity \(O(n^3)\):
for i in range(n):
for j in range(n):
for k in range(n):
print(i, j, k)Playing a Round of “Who’s Who?”
“Who’s Who” is a very simple party game. One player secretly picks a member of a large group. Then, another player in charge of guessing the selected player will ask a series of yes/no questions to proceed by elimination. The goal of the game is to find the selected person in as few questions as possible. The best questions, such as “does the selected person wear glasses?”, divide the group in half.
The following code implements a basic version of this game. Before reading on, can you find the cost associated with each line?
guests_not_eliminated = 100
while guests_not_eliminated > 1:
guests_not_eliminated = guests_not_eliminated // 2
print("selected person found")Expand to see the annotated snippet
The following costs are indicated as comments below:
guests_not_eliminated = 100 # cost: 1
while guests_not_eliminated > 1: # cost: log(n)
guests_not_eliminated = guests_not_eliminated // 2 # cost: log(n)
print("selected person found") # cost: 1Why would the while loop run \(\log(n)\) times? It will run until the number of guests not eliminated is \(1\). The while loop will run as many times as we need to divide the number of guests \(n\) by \(2\) before we reach \(1\).
Mathematically, we are solving the equation \(\frac{n}{2^k} = 1\).
In English, how many times (here \(k\)) do we need to divide \(n\) by \(2\) to get \(1\)?
Solving for \(k\) we get: \[\frac{n}{2^k} = 1\] \[2^k = n\] \[k = log(n)\]
Expressing the run time as a function of \(n\), we then get \(f(n) = 2 \cdot 1 + 2 \cdot \log(n)\), which is of complexity \(O(\log(n))\).
Taking Pictures
The last activity of this strange party was to take a picture of each possible combination of guests. The example below shows how the number of pictures increases with the number of guests:
- \(0\) guest: \(\{\}\), \(1\) photo with no one in it. Sad party.
- \(1\) guest: \(\{\}\), \(\{A\}\), \(2\) photos, the empty photo and a photo of guest \(A\).
- \(2\) guests: \(\{\}\), \(\{A\}\), \(\{B\}\), \(\{AB\}\), \(4\) photos.
- \(3\) guests: \(\{\}\), \(\{A\}\), \(\{B\}\), \(\{C\}\), \(\{AB\}\), \(\{BC\}\), \(\{AC\}\), \(\{ABC\}\), \(8\) photos.
Before reading on, try implementing this in Python, starting with the following guest list: ["A", "B", "C", "D"].
Expand to view the implementation
This is implemented in the following code snippet:
from itertools import combinations
guests = ["A", "B", "C", "D"]
n = len(guests)
for combination_size in range(n + 1):
for combination in combinations(guests, combination_size):
print(combination)Annotating the cost next to the code snippets, we get:
from itertools import combinations # cost: 1
guests = ["A", "B", "C", "D"] # cost: 1
n = len(guests) # cost: 1
for combination_size in range(n + 1): # cost: n + 1
for combination in combinations(guests, combination_size): # cost: see below
print(f"taking picture of {combination}") # cost: see belowThe cost of the following sub-snippet is not straightforward:
for combination in combinations(guests, combination_size):
print(f"taking picture of {combination}")This for loop will run once for each combination at a given combination size. Using the example of three guests ["A", "B", "C"] to illustrate this concept, the for loop will run:
- Once for combination size \(0\): \(\{\}\)
- Three times for combination size \(1\): \(\{A\}\), \(\{B\}\), \(\{C\}\)
- Three times for combination size \(2\): \(\{AB\}\), \(\{AC\}\), \(\{BC\}\)
- Once for combination size \(3\): \(\{ABC\}\)
The number of combinations of \(k\) items of a list of \(n\) items is also known as the binomial coefficient, frequently written \(nCk\) or \(\binom{n}{k}\), and referred to as “\(n\) choose \(k\)” in spoken English. It can be computed with the following formula:
\[\frac{n!}{k!(n - k)!}\]
What we would now need to find is the sum of all binomial coefficients from \(0\) to \(n\) included, noted:
\[\sum_{k=0}^{n} \binom{n}{k}\]
Which simplifies to \(2^n\).
Another possible derivation of \(2^n\) is to view the total number of combination as a tree, as each guest can be in or out of the picture. The picture below shows how a binary tree can be used to derivate all possible combinations. The leaves represent all of the possible combinations for three guests.
Using properties of a binary tree, a tree of depth \(3\) will have \(2^3=8\) leaves. More generally, a tree of depth \(n\) will have \(2^n\) leaves.
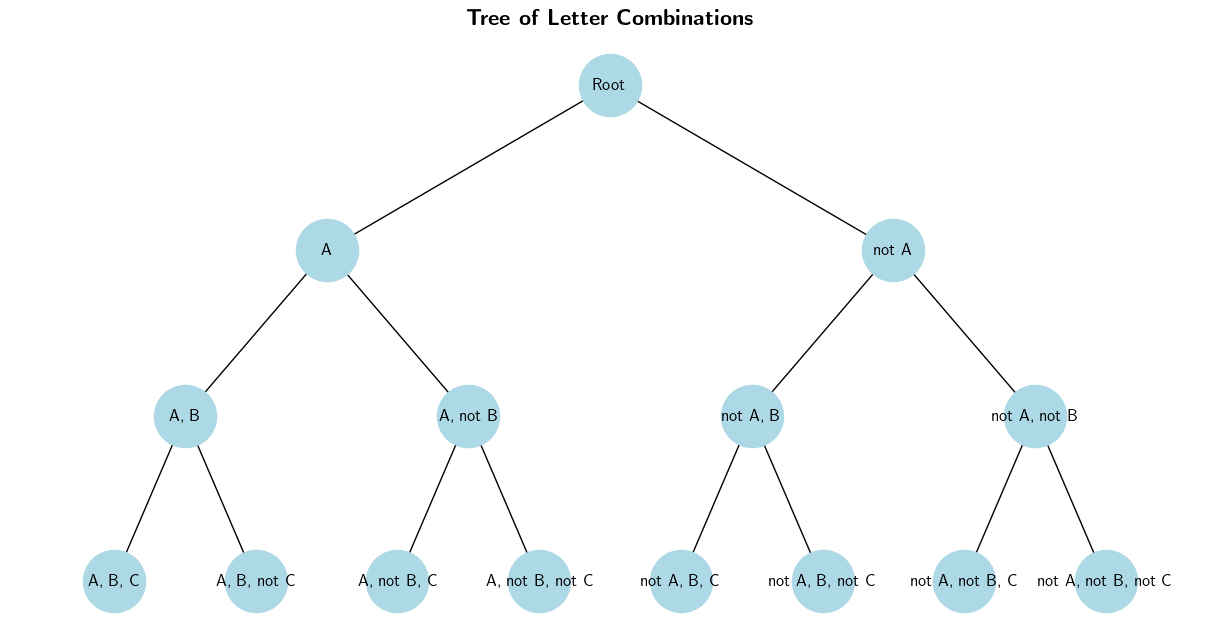
This can be derived intuitively by looking at the numbers of pictures required as the number of guests increases:
- \(0\) guest: \(\{\}\), \(1\) photo with no one in it. Sad party.
- \(1\) guest: \(\{\}\), \(\{A\}\), \(2\) photos, the empty photo and a photo of guest \(A\).
- \(2\) guests: \(\{\}\), \(\{A\}\), \(\{B\}\), \(\{AB\}\), \(4\) photos.
- \(3\) guests: \(\{\}\), \(\{A\}\), \(\{B\}\), \(\{C\}\), \(\{AB\}\), \(\{BC\}\), \(\{AC\}\), \(\{ABC\}\), \(8\) photos.
\(1, 2, 4, 8, ...\) is the sequence of the powers of \(2\): \(2^0, 2^1, 2^2, 2^3, ...\)
Concluding this section on pictures, the loop over all combinations for each combination size generates a complexity of \(O(2^n)\).
As already mentioned in part 1, this shows once again that such a task is not a fantastic idea.
Final Thoughts
With these simple examples in mind, you can now start analysing the complexity of your own code. As seen above, keep focussing on the bottlenecks of your programs. The complexity of a program is determined by the couple of lines with the highest cost as the input size tends towards infinity.
Can you eliminate a nested loop? Should you replace a list by priority queue? Can you store your observations in a KD-Tree? The world of Computer Science is full of opportunities for smarter solutions. Happy analysing!